This calculator computes the minimum sample size for your study using Cochran’s formula. With this calculator, you don’t have to worry about applying Cochran’s formula manually. Simply enter the confidence level (e.g., 95 for 95%), estimated proportion (p), and margin of error (e) to find the minimum sample size, assuming an infinite population. However, if you know the population size, make sure to specify it, and the calculator will apply the finite population correction.
Moreover, the calculator also provides a thorough explanation, showing how to apply your parameters in the Cochran’s formula to obtain the minimum sample size.
For another useful method, check out our Slovin’s Sample Size Calculator to compare different sample size calculations and determine the most suitable for your research.
How to Use Cochran’s Formula Calculator
Using the Cochran’s formula Calculator is simple. Follow these steps:
- Enter the confidence interval as an integer (e.g., 95 for 95% or 99 for 99%)
- Enter the estimated proportion (p) as a decimal. If you don’t know which value to use, use p = 0.5. Using 0.5 ensures that the resulting sample size is large enough to achieve the desired margin of error, regardless of what the actual population proportion turns out to be.
- Enter the margin of error (e) as a decimal (e.g., 0.05 for 5% margin of error).
- Click the Calculate button to compute the minimum sample size for an infinite population.
However, if the population is known and finite, the calculator will apply the finite population correction (FPC) and provide you with the minimum sample size after the correction.
Cochran’s Sample Size Formula
Cochran’s sample size formula is a statistical method used to calculate the ideal sample size for a study. It helps researchers determine how many participants they need to get accurate and reliable results.
The formula is widely used in surveys, experiments, and research where a random sample is needed. It ensures that the sample is large enough to represent the entire population while minimizing errors.
Cochran’s formula is:
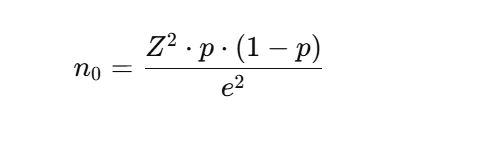
Where:
- Z is the Z-score (confidence level)
- p is the estimated proportion of the population
- e is the margin of error
Note. In some cases, 1-P is denoted by q.
Finite Population Correction (FPC)
When the population size (N) is not very large, the sample size should be adjusted using the Finite Population Correction (FPC) factor. This correction accounts for the fact that smaller populations require proportionally smaller samples.
Thus, the correct Cochran’s formula after finite population correction becomes:
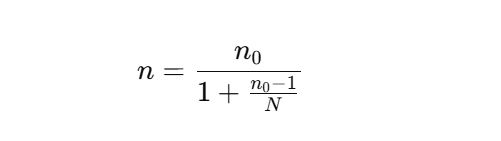
Where:
- n is the adjusted sample size
- n₀ is the initial sample size from Cochran’s formula
- N is the total population size
This adjustment ensures your sample remains representative even when dealing with limited or known populations.
Calculating Sample Size Using Cochran’s Formula: Step-by-Step Examples
Understanding the Cochran’s sample size formula is easier when you see it in action. Below are two practical examples that show how to calculate the sample size for both large and small populations, manually. The first example shows how to compute the Cochran’s sample size without the finite population correction (FPC), while the second one shows how to adjust the sample size using the finite population correction (FPC) factor. These examples will help you see exactly when and how to apply FPC for accurate results.
Example 1: Large Population (No FPC Needed)
Imagine a national researcher wants to find out how many adults in a country of over 100,000 people support a new health policy. Because the total population is large, we’ll assume it’s infinite (no finite population correction needed). The researcher wants results that are 95% confident, with a margin of error of 5%, and has no prior data on population proportion, so they use the most conservative estimate of p = 0.5.
Thus, from the scenario, we know that:
- Confidence Level = 95% → Z = 1.96
- Margin of Error = 5% → e = 0.05
- Estimated Proportion = 0.5
By definition, the Cochran’s formula for a large (infinite) population is:
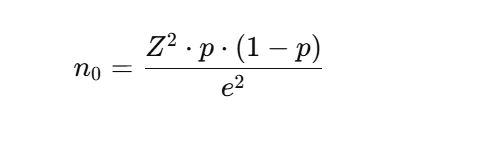
Substituting the given values, we have:
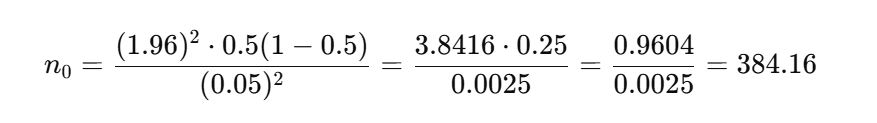
Thus, for a large or infinite population, the required sample size is approximately 384 respondents. This implies that surveying 384 people provides 95% confidence within a 5% margin of error.
Example 2: Small Population (With Finite Population Correction)
A researcher wants to estimate the level of job satisfaction among employees in a small company with 2,000 workers. The goal is to achieve a 95% confidence level and a 5% margin of error, with an estimated population proportion of p = 0.5. Because the total population (N = 2,000) is relatively small, we must apply the finite population correction (FPC) to get a more accurate sample size.
By definition, the Cochran’s formula after adjusting for the finite population correction is:
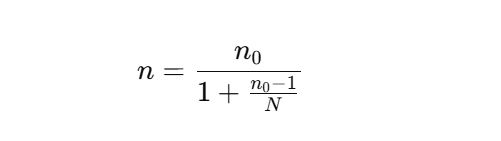
From the previous example, the sample size, n0 = 384.16
Substituting the values in the formula and solving, we have:
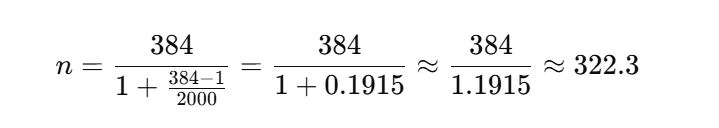
Therefore, for a population of 2,000 employees, the adjusted sample size is approximately 322 respondents. This clearly shows that by applying the finite population correction, the sample size is reduced from 384 to 322. This ensures accurate representation without oversampling.
Note. In many situations, you’ll be required to round up the sample size after calculation. This means rounding up to the nearest integer. Thus, for 384.16, the correct sample size becomes 385. Similarly, a sample size of 322.3, the rounded up sample size becomes 323.
Citation: Johnson, C. (2025) Cochran’s Sample Size Calculator, Dissertation Data Analysis Help. Available at: https://dissertationdataanalysishelp.com/cochrans-sample-size-calculator/ (Accessed: 03 November 2025).
Frequently Asked Questions
Cochran’s formula is used to calculate the ideal sample size for surveys and research. It helps ensure accurate results while minimizing errors.
You can manually calculate sample size using either Cochran’s formula or Slovin’s formula, depending on your research needs.
– Cochran’s formula is: n = (Z^2 * p * (1-p)) / e^2. This formula is best suited for large populations and when you have an estimated proportion (p).
– Slovin’s formula is: n = N / (1 + Ne²). This formula is useful when the population size (N) is known, but you do not have an estimated proportion
The minimum sample size depends on the confidence level, margin of error, and population characteristics. If unsure, using 30 or more is often recommended for statistical analysis.
Yes, Cochran’s formula works for both large and small populations. However, when the population size is small or known (usually less than 20,000), you should apply the Finite Population Correction (FPC) factor to adjust the sample size for better accuracy. The correction ensures that your sample size is not larger than necessary while still providing reliable results. The adjusted formula is: n = n0/1+(n0-1)/N
The margin of error represents how much you expect your sample results to differ from the true population value. It directly affects the required sample size in Cochran’s formula. A smaller margin of error (for example, 3%) means you want more precision, so you’ll need a larger sample size. Conversely, a larger margin of error (for example, 10%) allows for less precision, so a smaller sample size will be enough.






