Cochran’s Sample Size Calculator
A sample size calculator is a tool that helps researchers determine how many participants or data points they need for a study. Choosing the right sample size is important to ensure accurate and reliable results. Cochran’s sample size formula is one of the most widely used methods for calculating sample size in surveys and experiments. It helps researchers find the ideal sample size based on the confidence level, margin of error, and estimated population proportion. Determining the correct sample size is crucial in academic research. This is mainly because a sample that is too small may lead to inaccurate conclusions, while a sample that is too large can waste time and resources. Our Cochran’s Sample Size Calculator makes this process easy by providing instant calculations. This article explains the formula and offers a free calculator for quick and accurate sample size estimation.
What is Cochran’s Sample Size Formula?
Cochran’s sample size formula is a statistical method used to calculate the ideal sample size for a study. It helps researchers determine how many participants they need to get accurate and reliable results.
The formula is widely used in surveys, experiments, and research where a random sample is needed. It ensures that the sample is large enough to represent the entire population while minimizing errors.
The formula is:
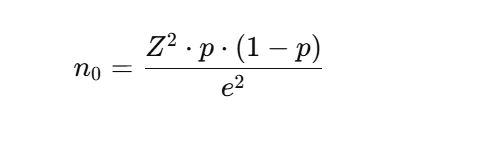
Where:
- Z is the Z-score (confidence level)
- p is the estimated proportion of the population
- e is the margin of error
Using this formula, researchers can find the correct sample size to improve the accuracy of their study.
How to Use Cochran’s Sample Size Calculator
Using Cochran’s Sample Size Calculator is simple. Follow these steps:
- Select a confidence level – Common choices are 90% (z score = 1.645), 95% (z score = 1.96), or 99% (z score = 2.58). A higher confidence level means greater accuracy but requires a larger sample.
- Enter the margin of error – This is the acceptable difference between the sample result and the actual population value (e.g., 5%).
- Set the estimated proportion (p) – If unsure, use 0.5, which gives the largest possible sample size.
- Calculate the sample size – The formula will determine the ideal sample size.
NOTE. If the population size is small, apply the finite population correction (FPC) to adjust the result. Choosing the right values ensures accurate research findings without unnecessary data collection.
Online Cochran’s Sample Size Calculator
Our online Cocran’s Sample Size Calculator makes it easy to find the right sample size for your study. Simply enter your values, and the tool will calculate the sample size instantly.
Sample Size Calculator using Cochran’s Method
Select the confidence level (90%, 95%, or 99%), enter the margin of error (e.g., 5%), and input the estimated proportion (default is 0.5 if unknown). If needed, enter the population size for small populations, then click “Calculate” to get the sample size.
Sample Size (n): –
For another useful method, check out our Slovin’s Sample Size Calculator to compare different sample size calculations and determine the most suitable for your research.
Conclusion
Determining the right sample size is essential for accurate research. Cochran’s sample size formula helps researchers calculate the ideal sample size based on confidence level, margin of error, and estimated proportion. Our Cochran’s Sample Size Calculator makes this process quick and easy.
Using the correct sample size improves the reliability of your study while avoiding unnecessary data collection. Try our Cochran’s Sample Size Calculator now and get instant results for your research!
Frequently Asked Questions
Cochran’s formula is used to calculate the ideal sample size for surveys and research. It helps ensure accurate results while minimizing errors.
You can manually calculate sample size using either Cochran’s formula or Slovin’s formula, depending on your research needs.
– Cochran’s formula is: n = (Z^2 * p * (1-p)) / e^2. This formula is best suitable for large populations and when you have an estimated proportion (p).
– Slovin’s formula is: n = N / (1 + Ne²). This formula is useful when the population size (N) is known, but you do not have an estimated proportion
The minimum sample size depends on the confidence level, margin of error, and population characteristics. If unsure, using 30 or more is often recommended for statistical analysis.
Yes, but for small populations, you should apply the finite population correction (FPC) factor to adjust the sample size for better accuracy.
